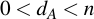http://www.johannes-bauer.com/compsci/ecc/ 에서 발췌
4 Doing useful ECC operations
4.1 Curve cryptosystem parameters
In order to turn all these mathematical basics into a cryptosystem, some parameters have to be defined that are sufficient to do meaningful operations. There are 6 distinct values for the Fp case and they comprise the so-called "domain parameters":
- p: The prime number which defines the field in which the curve operates, Fp. All point operations are taken modulo p.
- a, b: The two coefficients which define the curve. These are integers.
- G: The generator or base point. A distinct point of the curve which resembles the "start" of the curve. This is either given in point form G or as two separate integers gx and gy
- n: The order of the curve generator point G. This is, in layman's terms, the number of different points on the curve which can be gained by multiplying a scalar with G. For most operations this value is not needed, but for digital signing using ECDSA the operations are congruent modulo n, not p.
- h: The cofactor of the curve. It is the quotient of the number of curve-points, or #E(Fp), divided by n.
4.2 Generating a keypair
Generating a keypair for ECC is trivial. To get the private key, choose a random integer dA, so that
Then getting the accompanying public key QA is equally trivial, you just have to use scalar point multiplication of the private key with the generator point G:
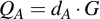
Note that the public and private key are not equally exchangeable (like in RSA, where both are integers): the private key dA is a integer, but the public key QA is a point on the curve.
'WHAT' 카테고리의 다른 글
| vmware tool 수동 설치 ubuntu server 18.04 (0) | 2019.03.29 |
|---|---|
| 크롬 컴파일 (0) | 2019.03.29 |
| pwn-pwnable [ringzer0team] (0) | 2015.06.14 |
| chal_rpc-pwnable [ringzer0team] (0) | 2015.06.11 |
| ask_grandpapa-coding [ringzer0team] (0) | 2015.06.11 |